Batch 3 - Class 153 - Shape of our Earth

• Write a program to simulate the above game of chance. Run a billion (or more!) games, and find the average payout. If you run enough games, you should be able to see that there are some of the outlier wins, that make it worth a large bet.

• How do we know that the earth is round, without using any technology? How would have the ancient greeks known it?
• It we kept traveling and never fell off? If we did fall off, it would mean that the earth is not round. If we didn't, the earth could still be flat and we might not have traveled far enough. This method doesn't work
• If we traveled around the earth in same direction and came back to the same point, then we would know. But how would we travel in the same direction without any technology?
• We could observe constellations from different parts of earth - they appear different, which would not happen if the earth was flat. Or angular position of north pole as you go from north to south.
• We could measure the length of shadow of a stick at different points at the same time. If earth was flat, all shadows would be the same length. Erastothenes did this in 200BC. 
• Ships disappearing on the horizon (bottom disappears first)
• One can define straight line as the shortest distance between two points. On a curved surface the shortest distance between two points is not a straight line when looked at from outside. 
• What is the shortest path between Tallahassee, Florida (Lat: 30.4, Long: 84.3 W) and Multan, Pakistan (Lat: 30.2, Long: 71.5 E)?
• The following figure shows the flight path from Delhi to San Francisco - why is the flight taking such a long path?

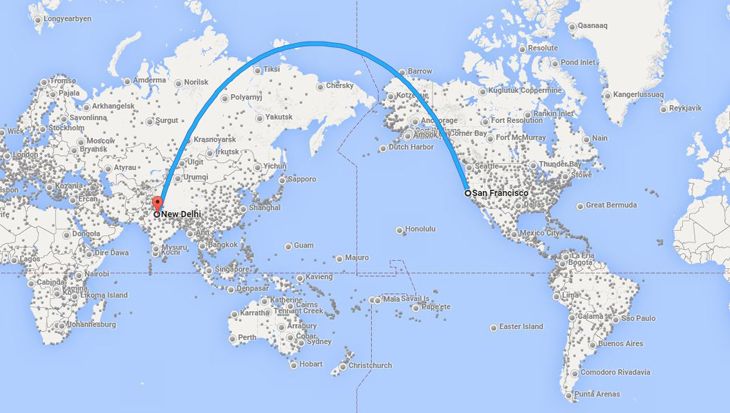
• Instructor Notes: Ask on a globe. If the impulsive answer is the latitude, then show that it can be smaller going through the north pole
• Great Circle Distance: There is a unique "great circle" through two points on a circle not opposite to each other. The shorter arc on this circle is the shortest path between the two points.
• What is "straight line" intrinsically on a sphere. If you start from Delhi, and keep walking in a "straight line" what does that mean? Is the equator an intrinsically straight path? Is the non-equator latitude between Tallahassee and Multan a straight path?
• We could define this as a bug walking so that both its legs are traveling the same distance. In that case, the great circle is the only straight path (but remember that there are infinite great circles through any single point)
• Mercator projection: Projection of world on a cylinder, so that constant latitude points are preserved. Note that the "plain paper map" is exactly that
• What is the scaling and inaccuracy? How does it change with latitude?
• What is the use of such a map?
• Straight lines on such a map (Rhumb lines) are good approximations for navigation.
• We could call a straight line on Mercator projection as a straight line, though it is not really the shortest path
• On surface of (perfectly spherical) earth, what would be the sum of angles of a triangle (formed by shortest paths between three points)
• Let kids draw some triangles on a globe and try
• The sum is greater than 180 degrees. For example if you take two longitudes through equator and meeting at north pole. 
• What can be the maximum sum? Since each angle has to be less than 180 degrees, the sum is less than 540 degrees
• On a spherical triangle, does SAS equivalence hold. i.e. if two sides and enclosed angle of two triangles on a sphere are the same, then are the triangles congruent
• Yes, the notion of where on the sphere you place this can be disregarded because you can always standardize of the equal sides as the "equator"
• Certain other equivalences like AAS do not hold, because sum of internal angles is not a constant unlike in planar geometry
• Does Pythagorus theorem hold on a sphere. If two short sides of a right angle triangle are 3 and 4, what is the long side. Equal to 5, less or more?
• Let kids think about it. Then measure on the sphere
• Given SAS equivalence, the answer must always be the same
• If the radius of sphere increases, which direction should this move in (Hint: think about what happens at infinite radius)
• On earth, if we traveled 30 miles west, then 30 miles north, then 30 miles east, and then 30 miles south, would be land up where we started? Why?
• What about 300 miles?
• What about 3000 miles? (Note: circumference of earth is about 25000 miles, radius 4000 miles)

• Is the surface of earth 2-dimensional or 3-dimensional?
• What is dimension?
• It is 2-dimensional, since all points on the surface can be expressed using two independent values (eg: latitude and longitude). It is, however, embedded in a 3-D space